Buenos días a todxs!
Ayer publicaban el siguiente artículo en agenciasinc.es, lo tenéis completo clicando aquí.
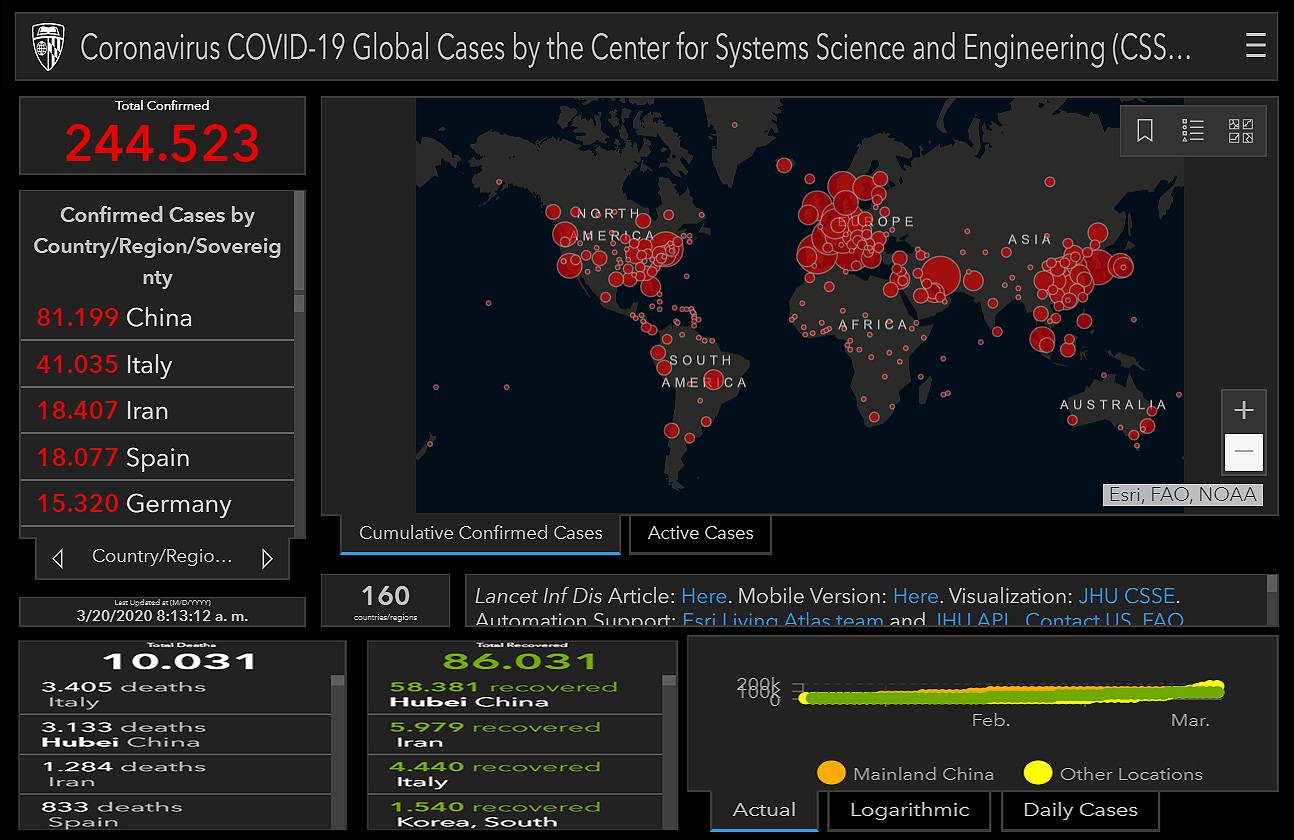
Como ya sabéis y se ha hablado del nuevo coronavirus SARS-Cov-2 las últimas semanas, es un virus que comenzó en China y que, en contra de lo que algunos pensaban, se ha probado que es de origen animal, este enlace habla de ello, con artículos de hace trece años hablando sobre el tema.
El objetivo que tenemos estos días es aplanar la curva de infectados diarios, es decir, bajar y retrasar lo máximo posible el pico para que no haya un colapso de los sistemas sanitarios.
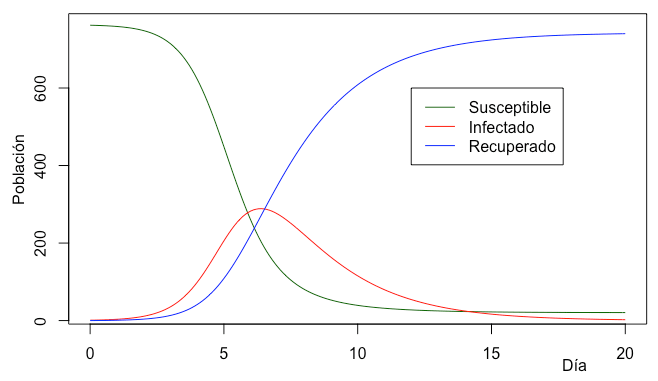
Tras las gráficas que nos han ido llegando por Whatsapp estos días hay modelos matemáticos que recogen características de los brotes epidémicos y permiten realizar predicciones. Uno de los más utilizados y con el que trabajamos hace un mes es el modelo SIR (Susceptibles de contraer la enfermedad, Infectados y Recuperados). Uno de los problemas que presenta utilizar este modelo, es que al ser nueva esta enfermedad los parámetros incluidos en el modelo se van estimando sucesivamente con los nuevos datos que se obtienen día a día, como puede ser R0.
El R0 del coronavirus, en circunstancias normales, ronda los 1.5 y 2.5, lo importante es reducirlo.
Una de las extensiones del modelo SIR es el SEIR, un sistema de ecuaciones donde se incorpora la población expuesta (E), aquellas personas que incuban el virus sin mostrar síntomas. Un grupo de investigadores de universidades gallegas y de Portugal lo han utilizado para modelizar la evolución de la pandemia y ayudar en la toma de decisiones. "Adaptándonos a las características propias del COVID-19, añadimos tres subpoblaciones (P de superpropagadores, A de afectados pero asintomáticos y H de hospitalizados) al modelo, con parámetros ajustados en función de los datos propios de este coronavirus desde que empezó en China", decía Juan José Nieto.
En base a los datos, estiman que "el pico se dará a principios de abril".
Otras herramientas matemáticas
El teorema de Bayes, que describe la probabilidad de un suceso basándose en el conocimiento previo de las condiciones relacionadas con ese suceso. Podríamos decir que va aprendiendo en función de los datos que conoce y esto aumenta la probabilidad de acertar. De León lo resume así "La información acerca de un determinado fenómeno tras el análisis de los datos, se obtiene actualizando los conocimientos previos con los nuevos datos".










