La geometría matemática de los alicatados

El reperterio ornamental hispanomusulmán se basa en tres elementos básicos de decoración: la epigrafía, la vegetación y la geometría. Todos ellos se encuentran magnificamente representados en la Alhambra. Hoy hablaremos de uno de estas decoraciones: la geométrica. La geometría es un concepto clave en el arte islámico pues no solo actúa como un elemento estilístico más, sino que está presente en todo el desarrollo arquitéctonico y ornamental como principio rector. Los diseños geométricos del arte nazarí se repiten en distintos formatos y superficies, pero quizá sean los alicatados uno de las principales manifestaciones de este tipo de ornamentación. Los alicatados están formados por pequeñas piezas de cerámica vidriada de diferentes formas y colores que se agrupan entre si para generar tramas geométricas de gran complejidad. El alicatado cumplía una doble función, decorativa, por un lado, y de protección de la superficie arquitectónica por otro. Los artesanos realizaban estos alicatados en función del sitio concreto que fueran a ocupar, eligiendo los grupos ornamentales que más se adecuaban a cada espacio. En la Alhambra se crearon gran variedad de tramas geométricas que fueron evolucionando en diseño y maestría a lo largo del tiempo. En el arte nazarí existen así composiciones simples, basadas en la repetición de uno o dos figuras; y composiciones complejas, en las que diferentes motivos se desplazan y rotan para generar a su vez nuevas formas geométricas a un nivel superior.
Los artesanos realizaban estos alicatados en función del sitio concreto que fueran a ocupar, eligiendo los grupos ornamentales que más se adecuaban a cada espacio. En la Alhambra se crearon gran variedad de tramas geométricas que fueron evolucionando en diseño y maestría a lo largo del tiempo. En el arte nazarí existen así composiciones simples, basadas en la repetición de uno o dos figuras; y composiciones complejas, en las que diferentes motivos se desplazan y rotan para generar a su vez nuevas formas geométricas a un nivel superior. Los entramados geométricos de la decoración del arte hispanomusulmán se basan en tres elementos claves para teselar el plano, es decir para cubrir una superficie usando polígonos sin dejar huecos. En concreto: 1. Un motivo poligonal como base de las composiciones. 2. La creación de composiciones a través de isometrías, es decir, de movimientos del plano de dichos motivos conservando sus proporciones. Esto se lleva a cabo mediante:
Los entramados geométricos de la decoración del arte hispanomusulmán se basan en tres elementos claves para teselar el plano, es decir para cubrir una superficie usando polígonos sin dejar huecos. En concreto: 1. Un motivo poligonal como base de las composiciones. 2. La creación de composiciones a través de isometrías, es decir, de movimientos del plano de dichos motivos conservando sus proporciones. Esto se lleva a cabo mediante:
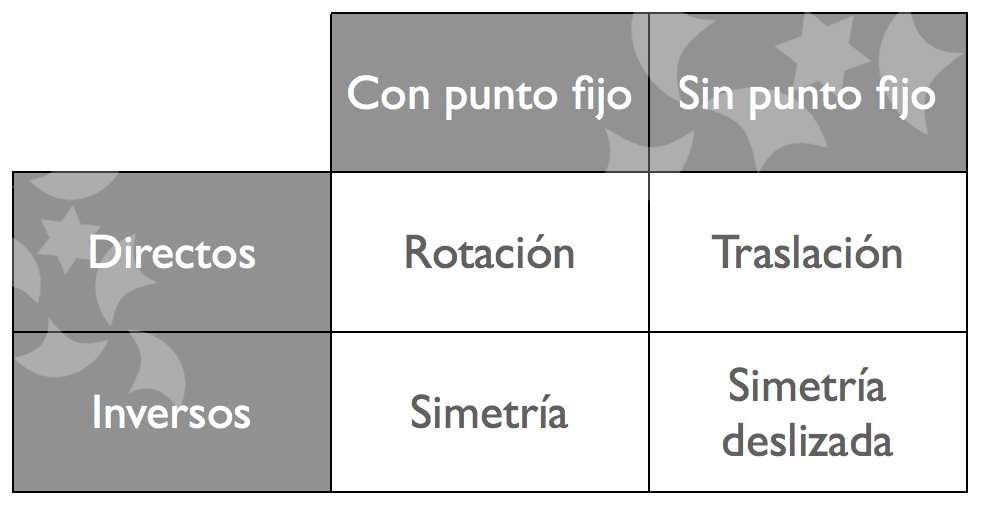
- Traslación: desplazamiento a una nueva posición fijo sin cambiar la orientación.
- Rotación: giro directo del motivo sobre un punto fijo.
- Simetría: reflexión o imagen especular inversa del motivo.
- Simetría deslizada: traslación de la reflexión en el mismo eje sin un punto fijo.
 3. El crecimiento lineal de dichas composiciones que se podría continuar hasta el infinito. Estas teselaciones pueden hacerse a través de motivos poligonales, más sencillas de realizar los que más abundan en los alicatados de la Alhambra; o de motivos no poligonales. Estas segundas implican una mayor maestría pues supone un proceso más laborioso de creación para conseguir formas no poligonales que encajen entre sí. Como ejemplo de formas no poligonales la más popular es la forma de trisquel o “pajarita”, creada a través de la tranformación de un triángulo equilátero.
3. El crecimiento lineal de dichas composiciones que se podría continuar hasta el infinito. Estas teselaciones pueden hacerse a través de motivos poligonales, más sencillas de realizar los que más abundan en los alicatados de la Alhambra; o de motivos no poligonales. Estas segundas implican una mayor maestría pues supone un proceso más laborioso de creación para conseguir formas no poligonales que encajen entre sí. Como ejemplo de formas no poligonales la más popular es la forma de trisquel o “pajarita”, creada a través de la tranformación de un triángulo equilátero. En geometría solo hay 17 grupos cristalográficos planos, es decir 17 formas de teselar un plano. Estos grupos cristalográficos fueron demostrados por el cristalógrafo ruso E.S. Fedorov en 1891, sin embargo todos ellos habían sido representadas con anterioridad en la Alhambra. Los artesanos nazaríes trazaron con tal maestría las representaciones geométricas que llegaron a generar todos los grupos de simetría posibles dejando un legado no solo ornamental, sino también matemático pues es el único monumento antiguo en el cual están presentes los 17 diseños. Estos grupos pueden ser agrupados en función del orden máximo de giros, así se generan:
En geometría solo hay 17 grupos cristalográficos planos, es decir 17 formas de teselar un plano. Estos grupos cristalográficos fueron demostrados por el cristalógrafo ruso E.S. Fedorov en 1891, sin embargo todos ellos habían sido representadas con anterioridad en la Alhambra. Los artesanos nazaríes trazaron con tal maestría las representaciones geométricas que llegaron a generar todos los grupos de simetría posibles dejando un legado no solo ornamental, sino también matemático pues es el único monumento antiguo en el cual están presentes los 17 diseños. Estos grupos pueden ser agrupados en función del orden máximo de giros, así se generan:
- Grupos de simetría sin giros: existiendo 4 grupos (en concreto, según la nomenclatura del sistema internacional abreviado: P1, cm, pg y pm)
- Grupos de simetría con giros de 180 grados: existiendo 5 tipos de simetría (P2, cmm, pmm, pmg, pgg)
- Grupos de simetría con giros de 120 grados: con 3 grupos de simetrías (P3, P31m, P3m1)
- Grupos de simetría con giros 90 grados: con 3 grupos (P4, P4m, P4g)
- Grupos de simetría con giros de 60 grados: con 2 grupos (P6, P6m)
En el arte nazarí las composiciones más populares son las de giros de 90º, aunque en la Alhambra todos los grupos se encuentran representados. Entre los alicatados del Museo de la Alhambra se encuentran ejemplos de estas formas de teselar un plano. . ¿Os animáis a profundizar en la geometría y buscar los grupos de simetría que se esconden en los alicatados del museo y de la Alhambra? . Os recomendamos una serie de artículos y recursos para profudizar en el tema: Garro Garro, Juan Carlos, Rojo Montijano, José: ”Un Mosaico para Dubai” Hernández Rojo, Fernando: “Desde el estudio de los elementos de simetría de los mosaicos de la Alhambra hasta la creación de nuevos diseños? Martínez Vela, Manuel: La Alhambra con regla y compás. Editorial Almizate – Patronato de la Alhambra y Generalife. 2017 Lovric, Miroslav: “Magic geometry: Mosaics un the Alhambra”. Pérez Gómez, Rafael: “Un matemático passeggia per l’Alhambra”. Pérez Gómez, Rafael: “The four regular mosaics missing in The Alhambra”. Movimientos en el plano. Aplicación al estudio de las Teselaciones en el plano. Frisos y Mosaicos
. ¿Os animáis a profundizar en la geometría y buscar los grupos de simetría que se esconden en los alicatados del museo y de la Alhambra? . Os recomendamos una serie de artículos y recursos para profudizar en el tema: Garro Garro, Juan Carlos, Rojo Montijano, José: ”Un Mosaico para Dubai” Hernández Rojo, Fernando: “Desde el estudio de los elementos de simetría de los mosaicos de la Alhambra hasta la creación de nuevos diseños? Martínez Vela, Manuel: La Alhambra con regla y compás. Editorial Almizate – Patronato de la Alhambra y Generalife. 2017 Lovric, Miroslav: “Magic geometry: Mosaics un the Alhambra”. Pérez Gómez, Rafael: “Un matemático passeggia per l’Alhambra”. Pérez Gómez, Rafael: “The four regular mosaics missing in The Alhambra”. Movimientos en el plano. Aplicación al estudio de las Teselaciones en el plano. Frisos y Mosaicos

















