𝐁𝐞𝐫𝐧𝐡𝐚𝐫𝐝 𝐑𝐢𝐞𝐦𝐚𝐧𝐧. Corta vida, amplias contribuciones

El 17 de septiembre de 1826 nacía el matemático alemán Bernhard Riemann. En su corta vida (fallecía con tan solo 39 años) realizó contribuciones fundamentales al análisis y la geometría diferencial.

En 1840, Riemann entró directamente en el tercer curso del Lyceum en Hannover. En 1842 ingresó en el Johanneum Gymnasium en Lüneburg, donde mostró particular interés por las #matemáticas y el director le permitió estudiar textos de su biblioteca particular.

Un dato curioso: Riemann leyó las 700 páginas de la Teoría de Números de Legendre en seis días.

En 1846, Riemann entró como estudiante en la Universidad de Gotinga, donde impartía clase 𝐆𝐚𝐮𝐬𝐬. Al año siguiente se cambió a la Universidad de Berlín, para continuar aprendiendo con 𝐒𝐭𝐞𝐢𝐧𝐞𝐫, 𝐉𝐚𝐜𝐨𝐛𝐢, 𝐃𝐢𝐫𝐢𝐜𝐡𝐥𝐞𝐭 𝐲 𝐄𝐢𝐬𝐞𝐧𝐬𝐭𝐞𝐢𝐧.

En 1849 volvió a Gotinga para trabajar en su Tesis Doctoral con Gauss, que versó sobre teoría de variable compleja, introduciendo métodos topológicos en su estudio. Describió lo que conocemos como 𝐒𝐮𝐩𝐞𝐫𝐟𝐢𝐜𝐢𝐞𝐬 𝐝𝐞 𝐑𝐢𝐞𝐦𝐚𝐧𝐧

La defendió el 16 de diciembre de 1851.

Gauss recomendó a Riemann que pidiera una plaza en Gotinga. Dedicó 30 meses a preparar su exposición para la Habilitación, sobre representación de funciones mediante series trigonométricas pero desde un punto de vista diferente a la expansión por 𝐬𝐞𝐫𝐢𝐞𝐬 𝐝𝐞 𝐅𝐨𝐮𝐫𝐢𝐞𝐫

Para la Habilitación, Riemann proporcionó las condiciones que tiene que cumplir una función para poseer una integral. Lo que hoy conocemos como condición de 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐛𝐢𝐥𝐢𝐝𝐚𝐝 𝐝𝐞 𝐑𝐢𝐞𝐦𝐚𝐧𝐧

También para la Habilitación, Riemann dio la definición de 𝐭𝐞𝐧𝐬𝐨𝐫 𝐝𝐞 𝐜𝐮𝐫𝐯𝐚𝐭𝐮𝐫𝐚. Propuso cuestiones importantes sobre la relación de la geometría con el mundo en que vivimos. Planteamiento muy avanzado para su época que muchos de sus contemporáneos no entendieron. Según Freudental, Einstein encontró en la teoría desarrollada por Riemann el marco perfecto para que encajaran sus ideas físicas, su cosmología y su cosmogonía. La aportación de Riemann fue justo lo que necesitaba la física: una estructura métrica determinada por los datos.

La hipótesis de Riemann es uno de los más conocidos problemas de #matemáticas. Afirma que la parte real de todo cero no trivial de la función zeta de Riemann es ½ pero no se ha podido probar. Es uno de los 𝐏𝐫𝐨𝐛𝐥𝐞𝐦𝐚𝐬 𝐝𝐞𝐥 𝐌𝐢𝐥𝐞𝐧𝐢𝐨 con importante premio económico

Leonhard Euler. Uno de los matemáticos más prolíficos y brillantes del siglo XVIII

Euler fue la primera persona que usó un grafo para resolver un problema. El problema al que me refiero, el que resolvió don Leonhard con un grafo, es un problema bien conocido en divulgación matemática: el problema de los puentes de Königsberg.

Viajamos al siglo XVIII.

En una ciudad prusiana llamada Könisberg -actualmente Kaliningrado- había 7 puentes.

La orografía de Könisberg era un tanto especial alrededor de los puentes, ya que la ciudad quedaba dividida en cuatro partes por el río Pregel.

Así 👇

En aquellos tiempos, alguien formuló la siguiente pregunta:

¿Es posible, comenzando en cualquier sitio de la ciudad de Könisberg, elegir un recorrido que nos permita pasar una única vez por cada uno de los siete puentes sobre el río Pregel?

Esta cuestión es conocida como el "Problema de los puentes de Könisberg".

Fíjense que en la pregunta anterior no se impone que el punto de inicio coincida con el punto final del recorrido.

Esa sería una pregunta diferente: ¿se puede diseñar un circuito, empezando y terminando en el mismo punto de la ciudad, que pase una, y solo una vez, por todos los puentes de Könisberg?

Las respuestas a estas dos preguntas se la debemos al protagonista de nuestro hilo: Leonhard Euler.

Para ello, en 1736, representó el problema con puntitos y rayas: un vértice (punto) por cada zona de la ciudad y una arista (rayita) entre dos de esas zonas por cada puente que las una.

La pregunta sobre Könisberg se transforma en la siguiente pregunta: ¿se puede dibujar ese grafo rojo sin levantar el lápiz del papel y sin repetir ninguna de las líneas? ¿Y empezando y terminando en el mismo vértice?

La respuesta a ambas preguntas es NO, según el teorema de Euler.

De hecho, en su honor, a los grafos que tienen la propiedad de poder ser recorridos (empezando y terminando en el mismo vértice) sin repetir aristas se les conoce como "grafos eulerianos".

Pues bien, un grafo es euleriano si -y solamente si- el número de aristas (rayitas) que salen de cada vértice es un número par.

Y un grafo tiene un camino euleriano (puede empezar en un vértice y terminar en otro) si -y solamente si- solo tiene 2 vértices de los que sale un número impar de aristas.

Por cierto, al número de rayitas que sale de un punto (vértice) se le llama valencia o grado del vértice.

Si miramos el grafo asociado a los puentes de Könisberg y las valencias de los vértices, vemos que de todas son impares.

Por lo tanto, NO es euleriano (no se puede diseñar un circuito -empezando y terminando en el mismo vértice- sin repetir aristas.

Tampoco sería posible diseñar un recorrido euleriano (con principio y final distintos) porque, como hemos dicho, solo se puede si el número de vértices de valencia impar es 2.

Oye, ¿y si solo hay 1 vértice de valencia impar en el grafo? Les dejo que lo piensen un rato…

Dibujen un grafo (puntos y rayas) con un solo vértice de valencia impar y comprueben si lo pueden recorrer completo sin pasar dos veces por la misma arista.

Ops, perdonen. ¿No les sale ningún grafo con un único vértice impar? Claro. Es IMPOSIBLE :)

La suma total de las valencias de un grafo es siempre un número par. Al sumar todas las valencias están contando las aristas (las rayitas) dos veces; les saldrá el número de aristas multiplicado por 2.

Esta propiedad se conoce como "el lema del apretón de manos" :)

Pero, como he dicho, a Euler le debemos un montón de resultados matemáticos más en un montón de áreas de las matemáticas y la física.

Le debemos también la maravillosa y voluptuosa identidad de Euler :_)

También, fue el primero en observar que el ortocentro, circuncentro y baricentro de un triángulo siempre están alineados.

Otra de sus aportaciones es la Teorema de Euler que nos permite obtener la relación entre los vértices, caras y aristas de un poliedro.

C - A + V = 2

Texto obtenido del twitter de la Mátematica y Divulgadora Clara Grima.

Estadísica y genética. Fisher

Ronald Aylmer Fisher nació en Londres el 17 de febrero de 1890, en el seno de una familia numerosa de clase media. Desde pequeño, tuvo grandes problemas de visión que marcaron su vida y, muy probablemente, su carácter.

Siempre destacó en matemáticas y en 1909 recibió una beca para estudiar en Cambridge, finalizando sus estudios en 1912, Fisher empezó a trabajar entonces como estadístico para la ciudad de Londres combinando este trabajo con la docencia en diversos colegios.

En 1917 se casó con su prometida, Ruth E. Guinnes, con la que tuvo dos hijos y seis hijas.

Entre 1919 y 1933 Fisher trabajó en la empresa Rothamsted Research fundada en 1843 y dedicada a la experimentación agrícola.

El tratamiento de los datos recopilados en la empresa a lo largo de los años y la necesidad de crear nuevos experimentos llevaron a Fisher al desarrollo de potentes herramientas estadísticas que se vieron reflejadas en una gran producción científica.

Especialmente destacables son dos de sus publicaciones: Statistical Methods for Research Workers y The Design of Experiments.

Statistical Methods for Research Workers fue publicado en 1925 y en él se acuña la idea de hipótesis nula y se populariza el uso del p-valor. Según Fisher, la hipótesis nula era aquella establecida por defecto y que había que rebatir a partir de los datos observados, utilizando para ello el conocido como p-valor. Y qué era el p-valor para Fisher? Pues, de forma resumida, era una estimación de la probabilidad de observar esos datos si se asumía como cierta la hipótesis de partida.

En este contexto Fisher desarrolla también el Análisis de la Varianza (ANOVA) para contrastar la existencia de diferencias entre tratamientos experimentales, una metodología que ha llegado prácticamente intacta hasta nuestros días.

Estas ideas convierten a Fisher en uno de los padres del contraste estadístico de hipótesis y fueron la base de uno de sus grandes enfrentamientos personales, su enemistad con Eagon Pearson y Jerzy Neyman.

Años más tarde, en 1935, Fisher publicaba The Design of Experiments en el que formaliza la idea y la importancia del correcto diseño experimental y lo dota de base matemática. En particular, Fisher pone de manifiesto la necesidad de controlar y reducir toda la variabilidad ajena a la condición experimental para, de ese modo, poder establecer relaciones de causalidad. Dentro de este libro Fisher incluyó su famoso ejemplo: The Lady tasting tea. En versión moderna, imaginad que quedáis a tomar una cerveza con una amiga y esta pide una clara con limón. Al llegar el camarero con la clara vuestra amiga se pone hecha una furia. Dice que el camarero le ha puesto el limón antes que la cerveza y ella ha pedido cerveza con limón y no limón con cerveza. A ti te explota la cabeza… ¿Cómo puede notar la diferencia? De hecho, no crees que sea capaz de notarla. Para resolver un problema similar (pero con té y leche) Fisher diseño una experimento que hoy en día se conoce como la prueba exacta o test hypergermetrico de Fisher y es ampliamente utilizado en genética. La idea era dividir los campos en parcelas que se alineaban en filas y columnas y aplicar los tratamientos de forma que cada uno apareciese una única vez en cada fila y una única vez en cada columna (vamos… algo parecido a hacer un sudoku). En ambos ejemplos lo más importante es la intuición detrás del diseño, ya que Fisher intentó controlar toda la variabilidad no relacionada con aquello que quería probar.

Pero no solo hizo avances en Estadística, sino también en las teorías sobre la evolución y la herencia genética publicando, en 1930, su libro The Genetical Theory of Natural Selection.

Uno de sus grandes enfrentamientos fue con Karl Pearson, otro de los grandes de la Estadística del siglo XX, y se extendió su relación con el hijo de Karl, Eagon Pearson y su colaborador Jerzy Neyman.

Fuente Ana

Un modelo, un teorema y teoría de juegos contra el coronavirus

Buenos días a todxs!

Ayer publicaban el siguiente artículo en agenciasinc.es, lo tenéis completo clicando aquí.

 

Como ya sabéis y se ha hablado del nuevo coronavirus SARS-Cov-2 las últimas semanas, es un virus que comenzó en China y que, en contra de lo que algunos pensaban, se ha probado que es de origen animal, este enlace habla de ello, con artículos de hace trece años hablando sobre el tema. 

El objetivo que tenemos estos días es aplanar la curva de infectados diarios, es decir, bajar y retrasar lo máximo posible el pico para que no haya un colapso de los sistemas sanitarios.

Tras las gráficas que nos han ido llegando por Whatsapp estos días hay modelos matemáticos que recogen características de los brotes epidémicos y permiten realizar predicciones. Uno de los más utilizados y con el que trabajamos hace un mes es el modelo SIR (Susceptibles de contraer la enfermedad, Infectados y Recuperados). Uno de los problemas que presenta utilizar este modelo, es que al ser nueva esta enfermedad los parámetros incluidos en el modelo se van estimando sucesivamente con los nuevos datos que se obtienen día a día, como puede ser R0.

El R0 del coronavirus, en circunstancias normales, ronda los 1.5 y 2.5, lo importante es reducirlo.

Una de las extensiones del modelo SIR es el SEIR, un sistema de ecuaciones donde se incorpora la población expuesta (E), aquellas personas que incuban el virus sin mostrar síntomas. Un grupo de investigadores de universidades gallegas y de Portugal lo han utilizado para modelizar la evolución de la pandemia y ayudar en la toma de decisiones. "Adaptándonos a las características propias del COVID-19, añadimos tres subpoblaciones (P de superpropagadores, A de afectados pero asintomáticos y H de hospitalizados) al modelo, con parámetros ajustados en función de los datos propios de este coronavirus desde que empezó en China", decía Juan José Nieto.

En base a los datos, estiman que "el pico se dará a principios de abril".

Otras herramientas matemáticas

El teorema de Bayes, que describe la probabilidad de un suceso basándose en el conocimiento previo de las condiciones relacionadas con ese suceso. Podríamos decir que va aprendiendo en función de los datos que conoce y esto aumenta la probabilidad de acertar. De León lo resume así "La información acerca de un determinado fenómeno tras el análisis de los datos, se obtiene actualizando los conocimientos previos con los nuevos datos".

Recopilación de datos COVID-19

Durante estos días os pido que recopiléis datos sobre el número de infectados, de muertos y dados de alta día a día por el coronavirus. Cuando acabe el estado de alarma representaremos y analizaremos los datos recogidos matemáticamente.

Día Internacional de las Matemáticas

Hace unos meses la ONU reconoció el 14 de marzo como el Día Internacional de las Matemáticas, antes conocido como día de pi y el nacimiento de Albert Einstein.

Pi es un número irracional, trascendente y que aparece en más lugares que en los libros de Matemáticas ;)

El número pi es conocido por todos, pero ¿conoces todas las aplicaciones que tiene en nuestro día a día el número π ?

En clase hicimos el ejemplo de la aguja de Buffon y sorprendió a los alumnxs, nunca te esperas dónde puede aparecer π

Otra de las aportaciones al día de pi de los alumnos de 1º de Bachillerato:

En el siguiente hilo de Twitter podéis encontrar el porqué del número pi en la fórmula del área del círculo.

Geometría 2º ESO

Cualquier ejercicio o duda que os surja al leer los ejemplos o al intentar hacer las tareas, mandadme un correo a prietogarcia.andrea@gmail.com con fotos, texto o audios con las dudas. 

Tutorial

- Teorema de Pitágoras

Ejercicios resueltos

- Teorema de Pitágoras

Geometría

Tutoriales

Repaso

- Dominio, recorrido y puntos de corte

- Simetría y periodicidad

- Monotonía y extremos relativos y absolutos

- Continuidad

Ejercicios resueltos

- Funciones I

- Funciones II

- Ecuaciones de la recta

Cualquier duda mandadme un mail a prietogarcia.andrea@gmail.com 

Geometría en el espacio

Teoría

- Vectores con ejemplos

- Espacio afín con ejemplos

- Problemas métricos

Resúmenes

- Resumen de Geometría con ejercicios resueltos

- Ecuaciones de la recta y el plano

- Posiciones relativas de rectas y planos

- Ángulos y distancias

Límites y continuidad

Esta semana empezaríamos nueva unidad didáctica: Límites y continuidad. Ya hemos hecho una introducción a las funciones, damos paso a trabajar con algunos nuevos conceptos y repasar varios ya conocidos.

Estos son los tutoriales donde tendréis todo el material explicado y con ejercicios resueltos para tener varios como ejemplo.

Cualquier duda que os surja tras haber visto todo lo que os he facilitado, podrá ser consultada a mi correo prietogarcia.andrea@gmail.com

Unidad didáctica: Límites y continuidad

- Tema completo

Documentos

- Límite de una función

- Continuidad de una función

- Resumen de la unidad

- Límites, continuidad y asíntotas

- Reglas básicas para el cálculo de límites

Ejercicios

- Límites de funciones, continuidad y ramas infinitas

- Límites y continuidad

- Asíntotas y ramas parabólicas

- Autoevaluación 

- Soluciones de la autoevaluación

Tutoriales

- Límites (todo en una carpeta)

- Funciones

- Límites

- Límites laterales y continuidad 

- Funciones exponenciales

¡Ánimo con el estudio y con esta unidad!

Coronavirus-Clases

Buenos días alumnxs,

Como ya os he comentado en el aula virtual y por gmail, debido a la situación originada por el coronavirus tanto vosotros como vuestras familias debéis tener en cuenta:

1. No son vacaciones, el proceso de enseñanza-aprendizaje continúa en casa. 

2. Todos contáis con conexión a internet, bien porque lo tenéis en casa o porque algún vecino os lo pueda proporcionar en estos momentos.

En este blog se creará durante estos días de confinamiento una entrada para cada curso, donde se subirán las tareas que debéis realizar y enviarme, así como material para poder seguir llevando el contenido de la asignatura al día.

Los ejercicios que os pida tendrán todas las instrucciones de lo que debéis hacer con ellos.

NOTA: Cualquier duda podéis enviármela por gmail, tanto en formato de foto, texto o audio. 

¡Mucho ánimo y entre todos pasaremos esta mala situación!

CODVID19 y Matemáticas

Después de que hace unas horas se decretase la pandemia global por corona virus, quería mostraros los resultados de dos matemáticas en relación con el tema, por que sí, las matemáticas también sirven para prevenir mayor número de contagios de una enfermedad (como vimos en entradas anteriores) o para predecir cómo va a evolucionar.  Aunque en estos momentos lo que recomienden las autoridades sanitarias es lo que hay que hacer y lo más recomendable es evitar el contacto social.

Introducimos el Dilema del prisionero. La conclusión básica de este planteamiento, muy conocido en Teoría de Juegos es que, en la mayoría de situaciones, la cooperación conduce al bien común (a cambio de pequeños sacrificios individuales). La situación es la siguiente: pensemos en dos personas A y B que están contagiados pero no presentan síntomas. En la siguiente tabla se muestran los posibles escenarios y consecuencias esperadas de cada caso.

(Este argumento es el que plantea Clara Grima y otros autores en el libro Las matemáticas vigilan tu salud)

Por tanto, no se trata de que tú no te contagies, sino de que no nos contagiemos ninguno.

Aislarse, en la medida de nuestras posibilidades, en estas circunstancias, como vacunarse, es un acto de altruismo que todos deberíamos hacer.

@AnaBayes controla de modelos matemáticos y nos cuenta esto:

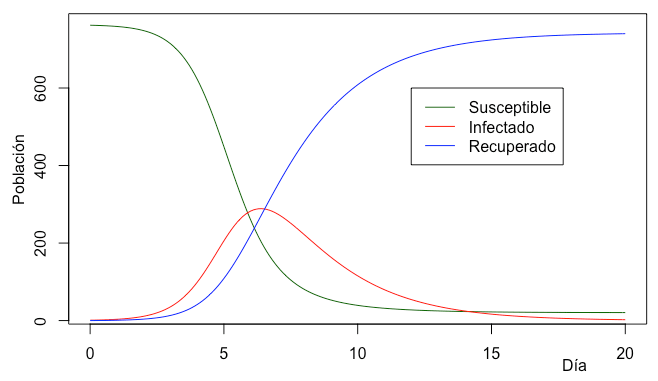
Imaginad un aula llena de personas donde 2 o 3 tienen la infección. Esas personas pueden contagiar a otras 2 personas cada una (en entradas anteriores ya vimos qué era R0). Si dejamos que el sistema se mueva sin hacer nada, efectivamente, los contagios crecerán de forma exponencial y, al final, todo el mundo estará contagiado. Sin embargo, solo hace falta un poco de control, aislar algunas zonas, para ver cómo el crecimiento se ralentiza muchísimo y dejamos de tener el famoso modelo exponencial. Si, además, metemos en la ecuación que a lxs enfermxs se les trata y se curan (en la mayor parte de los casos) eso genera otro cambio en el modelo que pasa a tener 3 tipos de personas, el modelo SIR (Susceptibles, Infectadas y Recuperados). Depende de cómo sea la enfermedad (y ahí es donde no tenemos datos) puede que las recuperadas vuelvan a ser susceptibles o no y eso también cambia el aspecto del sistema. En cualquier caso, lo importante es mantener la curva de infectados lo más plana posible para evitar el colapso del sistema

De la mano de @picanumeros tenemos lo siguiente:

La prevalencia de una enfermedad (E) es de 10 por cada 100.000 habitantes (0.01%). Aplicamos a una persona al azar un test que tiene una probabilidad del 99.9% de acertar. El test dice que la persona está enferma (A). ¿Cuál es la probabilidad de que la persona tenga realmente la enfermedad?

Recapitulemos: tanto la sensibilidad como la especificidad del test son del 99.9%, así que 

- la probabilidad de que dé positivo si está enferma es del 0.999, P(A|E) = 0.999.

- igual que la probabilidad de que dé negativo si no está enferma, P(A'|E')=0.999. (E' es el complementario de E, i.e., el suceso la persona No esté enferma y A' es el suceso el test dice que la persona no está enferma, el complementario del suceso A).

Si ya ha ocurrido A, buscamos entonces P(E|A). Aplicamos el Teorema de Bayes:

P(E|A) = P(A|E)*P(E) / [P(A|E)*P(E) + P(A|E')*P(E)]

Dado que P(A|E') = 1- P(A'|E') y P(E') = 1 - P(E), 

P(E|A) = 0.999*0.0001 + 0.001-0.9999 = 0.0908. 

La probabilidad de que la persona realmente tenga la enfermedad es de 0.0908 (9.08%), luego es mucho más probable que no la tenga. 

¿Cuál es el motivo de que sea tan baja? La prevalencia inicial.

Si aumentamos la prevalencia a 100 casos por cada 100.000 habitantes (0.1%), la probabilidad anterior aumentaría a 0.5 y, si lo hiciéramos a 1000 casos por cada 100.000 (1%), y sería de 0.91. ¿Verdad que te fiarías más de este test?

Si queremos elevar la probabilidad de que los positivos sean verdaderos hace falta elevar el valor predictivo del test, lo cual es más una cuestión técnica, pero también se puede elevar la probabilidad de estar enfermo a priori (seleccionando bien a quién se hace la prueba!!).

Esta selección a veces es complicada, por lo que hay estrategias para conseguir maximizar el éxito.

También, de mano de @AnaBayes, otro aspecto sería seguir la estrategia de repetir la prueba varias veces, incluso jugando con la sensibilidad y especifidad (siempre dentro de unos límites coherentes), para aumentar las posibilidades.